
Kublai: Hey, it’s you again! That formal verification thing you mentioned last time sucks!
Huh? You mean our proof of the ICan’tBelieveItCanSort algorithm?

Kublai: Yeah! ICan’tBelieveItCanSort? More like ICanBelieveItObviouslyCanSort! After watching that visualization a few times, it intuitively makes so much sense. It’s trivial.
Trivial? I’m banning that word. If you consider something to be trivial, you probably haven’t pondered it deeply enough.

Kublai: Seriously! I bet these formal verification tools like Dafny can only verify super trivial stuff, like “the sum of the concatenation of two sequences is equal to the sum of the sums of each sequence”.
Well, I’ll be happy to prove you wrong. Let’s verify a cool data structure using Dafny that you won’t be able to label as “trivial”: Fenwick trees, also known as binary indexed trees!

Fenwick: Hi! Did someone say my name? I’m Fenwick the rabbit!
Actually, Fenwick trees were first invented by Boris Ryabko, not Peter Fenwick (nothing is ever named after the first discover or inventor), so the name we’re using is a bit of a misnomer. Anyways, let’s try formally verifying them!

Kublai: Wait wait wait, what exactly is a Fenwick tree?
OK, so imagine you have an array A of size N with the following two operations:
void silly_update(int N, int *A, int i, int v) {
A[i] += v;
}
int silly_query(int N, int *A, int i) {
int ret = 0;
for (int j = 1; j <= i; j++)
ret += A[j];
return ret;
}

Fenwick: Note that we’ll use one-based indexing for the entirety of this post, since that’s what Fenwick trees traditionally use.
As you can see silly_update modifies an element in the array and silly_query returns the sum of all elements up to an index. How fast are they? silly_update is obviously super fast and runs in constant time. However, silly_query is not so great. If the query index is N, then silly_query will loop over the entire array! On average, it’ll take linear time!
Can we do better? Yes, using Fenwick trees, which can do both in logarithmic time!
void fenwick_build(int N, int *A, int *F) {
for (int i = 1; i <= N; i++) {
F[i] = A[i];
int j = i + (i & -i);
if (j <= N)
F[j] += F[i];
}
}
void fenwick_update(int N, int *F, int i, int v) {
for (; i <= N; i += i & -i)
F[i] += v;
}
int fenwick_query(int N, int *F, int i) {
int ret = 0;
for (; i; i -= i & -i)
ret += F[i];
return ret;
}

Kublai: That’s it? That’s like ten lines! Sure, there’s some crazy bit magic going on, but it’s probably pretty trivial.
No no no, Kublai. It’s some pretty deep stuff, trust me. I won’t explain here how Fenwick trees work, but you definitely need a solid intuitive understanding of them for the rest of this post. Here are some helpful resources:
- Brilliant.org
- An interactive visualization
- The intersecting chains property
- My previous blog post about some advanced Fenwick tree tricks
The journey begins

Kublai: (One hour later) Alright, I fully understand Fenwick trees now! Yeah, maybe they aren’t entirely trivial.
As far as I know, no one has formally verified Fenwick trees yet, although I did find a Why3 proof which appears to actually be for segment trees. In fact, Peter Fenwick’s original paper doesn’t even rigorously prove anything. He just describes his data structure and handwaves that it’s correct.
We’ll use the Dafny verification language, which I previously described in my ICanProveItCanSort! post. Fenwick trees might just be ten lines of code, but the formal proof is quite long and intricate, as in, uh… 350 lines long. And no, we’re not verifying some inefficient, recursive implementation of Fenwick trees. We’re going to verify that imperative implementation above with all its crazy loops.
The proof will use some fancy Dafny features, so if you’re not familiar with formal verification or Dafny, I recommend first reading this short post by Aaron Eline or the official Dafny guide.

Kublai: Whatever! I’m not scared! Bring on the proof!
Formalizing bit magic
Fenwick trees infamously use i & -i, which looks like evil bit magic but actually computes the least significant bit of i. You can also view this as the largest power of 2 that divides i. Unfortunately, Dafny only supports bitwise operations on bitvectors, not ints, but bitvectors are super gross. So, we’ll just have to implement our own version of i & -i:
opaque function lsb(i: int): int
requires i > 0
ensures 0 < lsb(i) <= i
{
if i % 2 == 1 then 1 else 2 * lsb(i / 2)
}
(Sorry about the bad syntax highlighting.1)

Kublai:
opaque? What’s that? I can’t even understand the first word of this proof!By default, Dafny aggressively inlines functions, but this causes performance problems in later parts of the proof. opaque disables that. The main consequence of opaque is that then Dafny won’t be able to peek inside the function to reason about it whenever we use it, so we’ll have to define a bunch of lsb lemmas to do that reasoning ourselves.
Anyways, the requires and ensures lines mean that the input to lsb must satisfy i > 0 and the return value is guaranteed to satisfy 0 < lsb(i) <= i. This is all proved by Dafny automatically!2

SHL: To check your understanding so far, explain why we needi > 0and why0 < lsb(i) <= ialways holds.
Now we’ll check lsb against i & -i for bitvectors.
lemma lsb_correct(i: int)
requires 0 < i < 65536
ensures lsb(i) == ((i as bv16) & -(i as bv16)) as int
{
reveal lsb;
}
This proof literally checks every value from 1 to 65535 and compares the two functions. The reveal is like the off switch for opaque and causes Dafny to repeatedly inline lsb in order to evaluate lsb(i).

SHL: Here’s another exercise. Convince yourself thatlsb(i)always equalsi & -ifor bitvectors of arbitrary size.
Defining the class
Dafny supports verifying object-oriented code, so we’ll now define a class called fenwick.
class fenwick {
// Size
var N: int
// It's a ghost spooky spooky
// "Ground truth" seq
// 0-indexed and size N
ghost var A: seq<int>
// FT array
// 1-indexed and size N + 1 for Fenwick reasons
// Sorry...
// const means we can modify F, but not reassign a completely new array to F
const F: array<int>
}

Kublai:
ghost? Yikes, I’m scared already!Don’t worry, ghost just means that the variable is only used for proof purposes and not actually included when you compile the program. In Dafny, a seq is immutable and an array is mutable. It’s easier for Dafny to reason about a seq compared to an array, which is why A is a seq. Also, ghost arrays are weird in Dafny and I couldn’t figure out how to modify an element in a ghost array.
Next, we’ll include a predicate (boolean function) in our class that checks that F is a valid Fenwick tree over A.
ghost predicate valid()
reads this
reads F
{
|A| == N && F.Length == N + 1 && forall i :: 0 < i <= N ==> F[i] == sum(A[i - lsb(i)..i])
}

Fenwick: Recall that the key property of Fenwick trees is thatF[i]stores the sum of the interval fromA[i - lsb(i) + 1]toA[i]inclusive!
I am very sorry to admit that I used zero-based indexing for A because it makes the code slightly cleaner, so it’s actually A[i - lsb(i)] to A[i - 1] since A is shifted over by one compared to F[i].
Lastly, we need to actually implement sum, so here’s a simple recursive implementation:
opaque ghost function sum(s: seq<int>): int
{
if |s| == 0 then 0 else s[0] + sum(s[1..])
}
Proving query
Now let’s prove something nontrivial! Here’s a simple member method that implements of query:
method query(i': int) returns (ret: int)
{
ret := 0;
var i := i';
while i > 0
{
ret := ret + F[i];
i := i - lsb(i);
}
}

SHL:
Convince yourself that the while loop terminates. Which property of lsb did we use?What conditions do we want query to satisfy? The state of the Fenwick tree should be valid and the return value should be sum(A[0..i']).
method query(i': int) returns (ret: int)
requires 0 < i' <= N
requires valid()
ensures ret == sum(A[0..i'])
{
ret := 0;
var i := i';
while i > 0
{
ret := ret + F[i];
i := i - lsb(i);
}
}
We’re not done yet! Dafny isn’t able to automatically prove that the ensures clause is satisfied, so we need to help it out.

Fenwick: Take a look at a Fenwick tree diagram and you’ll see that a query is just the union of some intervals! At each stepi, we can extend the intervals we’ve already covered. This is whyqueryworks.
method query(i': int) returns (ret: int)
requires 0 < i' <= N
requires valid()
ensures ret == sum(A[0..i'])
{
ret := 0;
var i := i';
assert ret == sum(A[i'..i']) by { reveal sum; }
while i > 0
invariant i >= 0 && ret == sum(A[i..i'])
{
ret := ret + F[i];
// Extend sum from i to i - lsb(i)
split(A, i - lsb(i), i, i');
i := i - lsb(i);
}
}

SHL:
Why do we need i >= 0 in the invariant? Explain what would happen if we removed it.We also need a “trivial” helper lemma for extending our current interval.
lemma split(A: seq<int>, i: int, j: int, k: int)
decreases |A| - i
requires 0 <= i <= j <= k <= |A|
ensures sum(A[i..j]) + sum(A[j..k]) == sum(A[i..k])
{
reveal sum;
if i < j {
split(A, i + 1, j, k);
}
}

Kublai: Cool proof, but that intuitively makes a lot of sense. Show me something cooler!
Proving update
Next, we’ll prove update.
method update(i': int, v: int)
{
var i := i';
while i <= N
{
F[i] := F[i] + v;
i := i + lsb(i);
}
}
Simple enough, right? Here are the specifications for what behavior we want. Again, we need the Fenwick tree to be valid. We’ll check that the update operation correctly updated A and that the Fenwick tree is still valid.
method update(i': int, v: int)
modifies this
modifies F
requires 0 < i' <= N
requires valid()
ensures A == old(A)[0..i' - 1] + [old(A)[i' - 1] + v] + old(A)[i'..]
ensures valid()
{
var i := i';
while i <= N
{
F[i] := F[i] + v;
i := i + lsb(i);
}
}

SHL: Convince yourself that those twoensuresclauses prevent us from cheating and modifyingFto just be a valid Fenwick tree but not the one that should be produced by addingvtoA[i' - 1].
A powerful lemma
We now need to prove a powerful and useful lemma about i + lsb(i), which is the parent of i in the update tree. The lemma states that lsb(i) < lsb(i + lsb(i)), namely that the lsb grows as you walk up the update tree.

SHL: Try proving this lemma mathematically.
Since lsb is always a power of 2, we can strengthen this lemma to 2 * lsb(i) <= lsb(i + lsb(i)). We’ll use this lemma pretty frequently. Here’s the proof, using induction:
lemma lsb_add(i: int)
requires i > 0
ensures 2 * lsb(i) <= lsb(i + lsb(i))
{
reveal lsb;
if i % 2 == 0 {
lsb_add(i / 2);
}
}
Here’s another lemma we’ll need for update that shows that no intervals between i and i + lsb(i) cover i:
lemma lsb_next(i: int)
requires i > 0
ensures forall j :: i < j < i + lsb(i) ==> j - lsb(j) >= i
{
reveal lsb;
}

SHL: Convince yourself that this lemma is true.
The actual proof
Now back to the body of the proof for update. First, let’s update the ground truth A:
A := A[0..i' - 1] + [A[i' - 1] + v] + A[i'..];
Now we’ll use our lemmas to show that only the parent of i' and the parent of the parent of i' and so on cover i', and those indices in F have been updated.
var i := i';
while i <= N
modifies F
decreases N - i
// Interval i always covers i'
invariant i - lsb(i) < i'
// F beyond i hasn't been modified
invariant forall j :: 0 < j < i' || i <= j <= N ==> F[j] == old(F[j])
// Only intervals covering i' have been modified so far
invariant forall j :: i' <= j < i && j <= N ==> if j - lsb(j) < i' then F[j] == old(F[j]) + v else F[j] == old(F[j])
{
F[i] := F[i] + v;
// Ensure lsb keeps getting bigger
lsb_add(i);
// Ensure the next interval covering i is at i + lsb(i)
lsb_next(i);
i := i + lsb(i);
}
// All intervals covering i' have been updated
assert forall i :: 0 < i <= N ==> if i - lsb(i) < i' <= i then F[i] == old(F[i]) + v else F[i] == old(F[i]);

SHL: Figure out which invariant is proved usinglsb_add(i)and which invariant is proved usinglsb_next(i).
Now we can check that all intervals before i' are unchanged:
forall i | 0 < i < i'
ensures F[i] == sum(A[i - lsb(i)..i])
{
assert A[i - lsb(i)..i] == old(A[i - lsb(i)..i]);
}
All the intervals after i':
forall i | 0 < i <= N && i - lsb(i) >= i'
ensures F[i] == sum(A[i - lsb(i)..i])
{
assert A[i - lsb(i)..i] == old(A[i - lsb(i)..i]);
}
And the intervals covering i', we’ll use a variant of split called split3:
lemma split3(A: seq<int>, i: int, j: int, k: int)
requires 0 <= i < j <= k <= |A|
ensures sum(A[i..j - 1]) + A[j - 1] + sum(A[j..k]) == sum(A[i..k])
{
reveal sum;
split(A, i, j - 1, k);
split(A, j - 1, j, k);
}
And here’s the proof for intervals covering i':
forall i | 0 < i <= N && i - lsb(i) < i' <= i
ensures F[i] == sum(A[i - lsb(i)..i])
{
// This is actually pretty simple but Dafny needs a lot of hand-holding
// Since we have to manually reason about sum
// Basically we use split3 to convince Dafny that the parts left and right of i' are unchanged
// And i' gets bumped up by v
calc == {
F[i];
old(F[i]) + v;
sum(old(A[i - lsb(i)..i])) + v;
{
assert sum(old(A)[i - lsb(i)..i' - 1]) + old(A)[i' - 1] + sum(old(A)[i'..i]) == sum(old(A[i - lsb(i)..i])) by {
split3(old(A), i - lsb(i), i', i);
}
}
sum(old(A)[i - lsb(i)..i' - 1]) + old(A)[i' - 1] + sum(old(A)[i'..i]) + v;
sum(old(A)[i - lsb(i)..i' - 1]) + A[i' - 1] + sum(old(A)[i'..i]);
{
assert A[i - lsb(i)..i' - 1] == old(A[i - lsb(i)..i' - 1]);
}
sum(A[i - lsb(i)..i' - 1]) + A[i' - 1] + sum(old(A)[i'..i]);
{
assert A[i'..i] == old(A[i'..i]);
}
sum(A[i - lsb(i)..i' - 1]) + A[i' - 1] + sum(A[i'..i]);
{
assert sum(A[i - lsb(i)..i' - 1]) + A[i' - 1] + sum(A[i'..i]) == sum(A[i - lsb(i)..i]) by {
split3(A, i - lsb(i), i', i);
}
}
sum(A[i - lsb(i)..i]);
}
}
And we’re done!

Kublai: Gah, my brains, they’re melting!
Well hey, you wanted to prove something nontrivial, right?

SHL: Kublai, I bet you didn’t do any of my exercises!
Proving the constructor
And now for the grand finale, we’ll prove a class constructor that builds F from an input sequence A'!
constructor (A': seq<int>)
{
N := |A'|;
A := A';
F := new int[|A'| + 1](i => 0);
new;
for i := 1 to F.Length {
F[i] := F[i] + A'[i - 1];
var j := i + lsb(i);
if j < F.Length {
F[j] := F[j] + F[i];
}
}
}

SHL: Convince yourself that this constructor is equivalent to starting with an all-zeroFand applyingupdateNtimes.

SHL: Compare the time complexities of this constructor versus applyingupdateNtimes.
As usual, here are the ensures clauses that we need:
constructor {:isolate_assertions} (A': seq<int>)
// https://dafny.org/latest/HowToFAQ/FAQUpdateArrayField
ensures fresh(F)
ensures A == A'
ensures valid()
{
N := |A'|;
A := A';
F := new int[|A'| + 1](i => 0);
new;
for i := 1 to F.Length {
F[i] := F[i] + A'[i - 1];
var j := i + lsb(i);
if j < F.Length {
F[j] := F[j] + F[i];
}
}
}
That loop looks pretty short and innocuous, but it’s actually extremely difficult to prove its correctness. This is because we have to specify the complete state at iteration i as some invariants. For a given i, we have forall j :: 0 < j < i ==> F[j] == sum(A[j - lsb(j)..j]), cool, but the js beyond i are potentially messed up by F[j] := F[j] + F[i] from previous loop iterations, and it’s very tricky to capture this state.
Some magic invariants
It turns out that these are the loop invariants we need:
// Everything up to i is good
invariant forall j :: 0 < j < i ==> F[j] == sum(A[j - lsb(j)..j])
// Future stuff is blank
invariant forall j :: i <= j <= N && j - lsb(j) / 2 >= i ==> F[j] == 0
// Uhhhhhhh
// The intervals covering i are in some pretty complicated state
// Not sure why it's j + (lsb(j + 1) / 2 >= i other than that it works
invariant forall j :: 0 < j < i && j + (lsb(j) + 1) / 2 >= i && j + lsb(j) <= N ==> lsb(j) < lsb(j + lsb(j)) && F[j + lsb(j)] == sum(A[j + lsb(j) - lsb(j + lsb(j))..j])

Kublai: Ah!!! It’s so scary! I can’t take it anymore!

SHL: Convince yourself that these invariants are–eh, forget it, even I don’t know the answer.

Fenwick: Hey! I can help. Consider this diagram ofF[48]and its children. Recall that the parent of a nodeiisi + lsb(i).
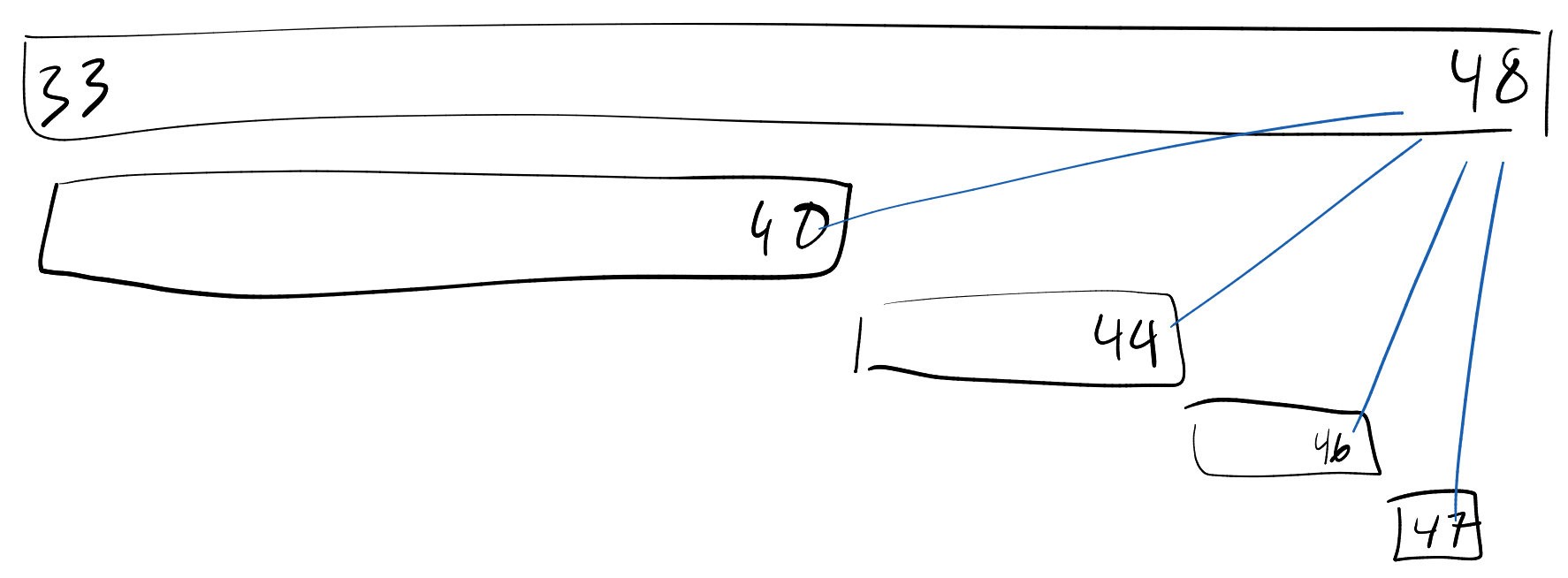

Fenwick: As you can seeF[48]will first get updated wheniis 40 which has parent 48. Thus,jwill not be updated until we reachi == j - lsb(j) / 2.
The third invariant is very complicated and magical so don’t worry about understanding it.

Kublai: Phew, looking at that invariant just makes my brain hurt.
More random lemmas
We now need some more lemmas for reasoning about a node and its children. Our first lemma is that if the intervals for i and its parent start at the same place, then i is the first child of its parent.
lemma lsb_no_par(i: int, j: int)
requires 0 < j < i
requires i - lsb(i) == i + lsb(i) - lsb(i + lsb(i))
ensures j + lsb(j) != i + lsb(i)
{
reveal lsb;
lsb_add(j);
}

SHL: Use the diagram withF[48]to intuitively see why this is true. Then, mathematically prove this usinglsb_add.
Next, we’ll consider if i is not the first child of its parent. If the interval for i starts after the interval for its parent, then i - lsb(i) also has the same parent.
lemma lsb_shared_par(i: int)
requires i > 0
requires i - lsb(i) > i + lsb(i) - lsb(i + lsb(i))
ensures i - lsb(i) + lsb(i - lsb(i)) == i + lsb(i)
{
reveal lsb;
if i % 2 == 0 {
lsb_shared_par(i / 2);
}
}

SHL: Mathematically prove this lemma.
This last lemma is a bit mysterious, but it basically ensures that if j is pretty close to its parent, then its parent cannot be i + lsb(i).
lemma lsb_bad_par(i: int, j: int)
requires 0 < j < i
requires j + (lsb(j) + 1) / 2 > i
ensures j + lsb(j) != i + lsb(i)
{
reveal lsb;
}
Using the lemmas and invariants
We now have everything we need to prove the constructor! Let’s add in the loop invariants.
for i := 1 to F.Length
modifies F
// Don't change A
invariant A == A'
// These three invariants are all interlocking
// Yeah it's super complicated, sorry
// Everything up to i is good
invariant forall j :: 0 < j < i ==> F[j] == sum(A[j - lsb(j)..j])
// Future stuff is blank
invariant forall j :: i <= j <= N && j - lsb(j) / 2 >= i ==> F[j] == 0
// Uhhhhhhh
// The intervals covering i are in some pretty complicated state
// Not sure why it's j + (lsb(j + 1) / 2 >= i other than that it works
invariant forall j :: 0 < j < i && j + (lsb(j) + 1) / 2 >= i && j + lsb(j) <= N ==> lsb(j) < lsb(j + lsb(j)) && F[j + lsb(j)] == sum(A[j + lsb(j) - lsb(j + lsb(j))..j])
{
F[i] := F[i] + A'[i - 1];
var j := i + lsb(i);
if j < F.Length {
F[j] := F[j] + F[i];
}
}
Unfortunately, Dafny has some performance issues when dealing with these super complicated loop invariants and might overheat or OOM your computer, so I added {:isolate_assertions} to the top of the constructor which speeds up verification.

Kublai: My brain is overheating too!
Don’t worry, I have another trick up my sleeve! One reason why Dafny is slow is because it assumes the loop invariant holds for i and tries to prove that the invariant now holds for i + 1 after the loop body. However, we haven’t filled in the proof for the loop body yet so of course it won’t be able to prove that, no matter how much it overheats your computer. Instead, we’ll comment out the invariants for now and add the invariants as assumptions to the beginning of the loop:
assume forall j :: 0 < j < i ==> F[j] == sum(A[j - lsb(j)..j])
assume forall j :: i <= j <= N && j - lsb(j) / 2 >= i ==> F[j] == 0
assume forall j :: 0 < j < i && j + (lsb(j) + 1) / 2 >= i && j + lsb(j) <= N ==> lsb(j) < lsb(j + lsb(j)) && F[j + lsb(j)] == sum(A[j + lsb(j) - lsb(j + lsb(j))..j])
Now we’re ready for the loop body! First, we’ll prove that with these assumptions, adding A'[i - 1] to F[i] will result in F[i] == sum(A[i - lsb(i)..i]).
// Get initial state of F[i]
if lsb(i) == 1 {
assert F[i] == sum(A[i - lsb(i)..i - 1]) by { reveal sum; }
} else {
assert lsb(i - 1) == 1 by { reveal lsb; }
}
assert F[i] == sum(A[i - lsb(i)..i - 1]);
assert A'[i - 1] == sum(A[i - 1..i]) by { reveal sum; }
split(A, i - lsb(i), i - 1, i);
F[i] := F[i] + A'[i - 1];
// Yay F[i] is good now
assert F[i] == sum(A[i - lsb(i)..i]);
Next comes the crazy part. If j is valid, then either i is its parent’s first child or i is a later child and i - lsb(i) is the previous child.
var j := i + lsb(i);
if j < F.Length {
F[j] := F[j] + F[i];
lsb_add(i);
if i - lsb(i) == j - lsb(j) {
// No prev child
} else {
assert i - lsb(i) > j - lsb(j);
// i - lsb(i) is prev child
}
}
For case 1, i is the first child. Here, we use lsb_no_par to ensure we didn’t mess up any js for the third loop invariant.
// No prev child
assert F[j] == F[i];
assert j - lsb(j) / 2 <= i;
assert F[j] == sum(A[j - lsb(j)..i]);
assert i + lsb(i) / 2 >= i && i + lsb(i) <= N;
assert i + lsb(i) / 2 >= i && i + lsb(i) <= N ==> F[i] == sum(A[j - lsb(j)..i]);
// Didn't break anything, hopefully
assert forall j :: 0 < j <= i && j + (lsb(j) + 1) / 2 > i && j + lsb(j) <= N ==> lsb(j) < lsb(j + lsb(j)) && F[j + lsb(j)] == sum(A[j + lsb(j) - lsb(j + lsb(j))..j]) by {
assert i + (lsb(i) + 1) / 2 >= i && i + lsb(i) <= N ==> lsb(i) < lsb(i + lsb(i)) && F[i + lsb(i)] == sum(A[i + lsb(i) - lsb(i + lsb(i))..i]);
forall j | 0 < j < i && j + (lsb(j) + 1) / 2 > i && j + lsb(j) <= N
ensures lsb(j) < lsb(j + lsb(j)) && F[j + lsb(j)] == sum(A[j + lsb(j) - lsb(j + lsb(j))..j])
{
lsb_no_par(i, j);
}
}
For case 2, we extend j’s interval from sum(A[j - lsb(j)..i - lsb(i)]) to sum(A[j - lsb(j)..i]) and use lsb_bad_par to also ensure we didn’t mess up the third loop invariant.
assert i - lsb(i) > j - lsb(j);
// i - lsb(i) is prev child
lsb_shared_par(i);
assert lsb(i - lsb(i)) >= 2 * lsb(i);
// Extend from i - lsb(i) to i
split(A, j - lsb(j), i - lsb(i), i);
assert F[j] == sum(A[j - lsb(j)..i]);
// Didn't break anything, hopefully
assert forall j :: 0 < j <= i && j + (lsb(j) + 1) / 2 > i && j + lsb(j) <= N ==> lsb(j) < lsb(j + lsb(j)) && F[j + lsb(j)] == sum(A[j + lsb(j) - lsb(j + lsb(j))..j]) by {
assert i + (lsb(i) + 1) / 2 >= i && i + lsb(i) <= N ==> lsb(i) < lsb(i + lsb(i)) && F[i + lsb(i)] == sum(A[i + lsb(i) - lsb(i + lsb(i))..i]);
forall j | 0 < j < i && j + (lsb(j) + 1) / 2 > i && j + lsb(j) <= N
ensures lsb(j) < lsb(j + lsb(j)) && F[j + lsb(j)] == sum(A[j + lsb(j) - lsb(j + lsb(j))..j])
{
lsb_bad_par(i, j);
}
}
And that’s it! Now we can delete the assume statements from earlier and add back in the loop invariants. Dafny can automatically prove the first and second loop invariants are maintained. We just needed to help it out for the weird third invariant.

Kublai: Alright, you win. That was pretty nontrivial!
Running the code
There you go! That’s the proof! Now we can try out our lovely formally verified Fenwick tree with a small example program:
method Main() {
var A := [1, 5, 3, 14, -2, 4, -3];
var FT := new fenwick(A);
var a := FT.query(5);
assert a == sum(A[0..5]);
print a, "\n";
ghost var B := FT.A[0..5];
assert B[0..5] == FT.A[0..5];
FT.update(3, 7);
var b := FT.query(5);
print b, "\n";
split3(B, 0, 3, 5);
split3(FT.A, 0, 3, 5);
assert B[0..2] == FT.A[0..2];
assert B[3..5] == FT.A[3..5];
assert a + 7 == b;
}
To run a Dafny program, Dafny first translates the program into a conventional language such as C# or Rust, and then uses the compiler for that language. Here’s the intermediate Rust code that our proof and program gets translated into, with some of the boilerplate removed. As you can see, all the ghost state and lemmas have been removed, and we’re left with something like the C code I showed at the very start of this post.
pub mod _module {
pub struct _default {}
impl _default {
/// fenwick.dfy(10,1)
pub fn lsb(i: &DafnyInt) -> DafnyInt {
let mut _accumulator: DafnyInt = int!(1);
let mut _r0 = i.clone();
'TAIL_CALL_START: loop {
let i = _r0;
if euclidian_modulo(i.clone(), int!(2)) == int!(1) {
return int!(1) * _accumulator.clone();
} else {
_accumulator = _accumulator.clone() * int!(2);
let mut _in0: DafnyInt = euclidian_division(i.clone(), int!(2));
_r0 = _in0.clone();
continue 'TAIL_CALL_START;
}
}
}
/// fenwick.dfy(336,1)
pub fn Main(_noArgsParameter: &Sequence<Sequence<DafnyChar>>) -> () {
let mut A: Sequence<DafnyInt> = seq![int!(1), int!(5), int!(3), int!(14), int!(-2), int!(4), int!(-3)];
let mut FT: Object<fenwick>;
let mut _nw0: Object<fenwick> = fenwick::_allocate_object();
fenwick::_ctor(&_nw0, &A);
FT = _nw0.clone();
let mut a: DafnyInt;
let mut _out0: DafnyInt = rd!(FT).query(&int!(5));
a = _out0.clone();
print!("{}", DafnyPrintWrapper(&a));
print!("{}", DafnyPrintWrapper(&string_of("\n")));
rd!(FT).update(&int!(3), &int!(7));
let mut b: DafnyInt;
let mut _out1: DafnyInt = rd!(FT).query(&int!(5));
b = _out1.clone();
print!("{}", DafnyPrintWrapper(&b));
print!("{}", DafnyPrintWrapper(&string_of("\n")));
return ();
}
}
/// fenwick.dfy(121,1)
pub struct fenwick {
pub N: ::dafny_runtime::Field<DafnyInt>,
pub F: ::dafny_runtime::Field<Object<[DafnyInt]>>
}
impl fenwick {
/// Allocates an UNINITIALIZED instance. Only the Dafny compiler should use that.
pub fn _allocate_object() -> Object<Self> {
allocate_object::<Self>()
}
/// fenwick.dfy(148,5)
pub fn _ctor(this: &Object<fenwick>, _A_k: &Sequence<DafnyInt>) -> () {
let mut _set_N: bool = false;
let mut _set_F: bool = false;
update_field_mut_uninit_object!(this.clone(), N, _set_N, _A_k.cardinality());
let mut _init0: Rc<dyn ::std::ops::Fn(&nat) -> DafnyInt> = {
Rc::new(move |i: &nat| -> DafnyInt{
int!(0)
})
};
let mut _nw0: Object<[MaybeUninit<DafnyInt>]> = array::placebos_usize_object::<DafnyInt>(DafnyUsize::into_usize(_A_k.cardinality() + int!(1)));
for __i0_0 in integer_range(0, rd!(_nw0.clone()).len()) {
{
let __idx0 = DafnyUsize::into_usize(__i0_0.clone());
::dafny_runtime::md!(_nw0)[__idx0] = MaybeUninit::new((&_init0)(&int!(__i0_0.clone())));
}
}
update_field_mut_uninit_object!(this.clone(), F, _set_F, array::construct_object(_nw0.clone()));
let mut _hi0: DafnyInt = int!(rd!(read_field!(rd!(this.clone()).F)).len());
for i in integer_range(int!(1), _hi0.clone()) {
{
let __idx0 = DafnyUsize::into_usize(i.clone());
::dafny_runtime::md!(::dafny_runtime::read_field!(::dafny_runtime::rd!(this.clone()).F))[__idx0] = rd!(read_field!(rd!(this.clone()).F))[DafnyUsize::into_usize(i.clone())].clone() + _A_k.get(&(i.clone() - int!(1)));
};
let mut j: DafnyInt = i.clone() + _default::lsb(&i);
if j.clone() < int!(rd!(read_field!(rd!(this.clone()).F)).len()) {
{
let __idx0 = DafnyUsize::into_usize(j.clone());
::dafny_runtime::md!(::dafny_runtime::read_field!(::dafny_runtime::rd!(this.clone()).F))[__idx0] = rd!(read_field!(rd!(this.clone()).F))[DafnyUsize::into_usize(j.clone())].clone() + rd!(read_field!(rd!(this.clone()).F))[DafnyUsize::into_usize(i.clone())].clone();
}
}
}
return ();
}
/// fenwick.dfy(231,5)
pub fn update(&self, _i_k: &DafnyInt, v: &DafnyInt) -> () {
let mut i: DafnyInt = _i_k.clone();
while i.clone() <= read_field!(self.N) {
{
let __idx0 = DafnyUsize::into_usize(i.clone());
::dafny_runtime::md!(::dafny_runtime::read_field!(self.F))[__idx0] = rd!(read_field!(self.F))[DafnyUsize::into_usize(i.clone())].clone() + v.clone();
};
i = i.clone() + _default::lsb(&i);
};
return ();
}
/// fenwick.dfy(316,5)
pub fn query(&self, _i_k: &DafnyInt) -> DafnyInt {
let mut ret: DafnyInt = int!(0);
let mut i: DafnyInt = _i_k.clone();
while int!(0) < i.clone() {
ret = ret.clone() + rd!(read_field!(self.F))[DafnyUsize::into_usize(i.clone())].clone();
i = i.clone() - _default::lsb(&i);
};
return ret.clone();
}
}
impl UpcastObject<DynAny>
for fenwick {
UpcastObjectFn!(DynAny);
}
}
And here’s the full proof in one gigantic file.
Conclusion
Anyways, if you made it this far and understood everything, congrats! You know the proof even better than I do! I’ll admit there are some lines of the proof where I have no idea what’s going on, but Dafny seems convinced.

Kublai: Oh wow, it’s over, it’s finally over!
I ran git log --numstat | rg fenwick.dfy | awk '{s+=$1;t+=$2} END {print s, t}' which reported back 1088 732, so it definitely took me a lot of tries and trial-and-error for this proof, especially for the constructor. I spent around 15 hours writing the proof.
I have a lot of other work that I probably should be doing instead, but writing Dafny code is sometimes kind of… fun? It’s like solving logic puzzles or puzzle games (Although maybe if you’re developing software, you don’t want it to be like solving logic puzzles or math problems). I’m a huge fan of puzzle games so this brought back a similar feeling. I also felt gravitated towards proving Fenwick trees because their implementation is so simple and elegant and concise, so they can’t be that hard to prove, right?

Fenwick: Yeah, it’s just 10 lines of code! You really can’t prove 10 lines? Come on!
Easier said than done, you know.
The final proof isn’t terribly long but it’s also not particularly insightful in my opinion. Still, I learned a lot about Fenwick trees from writing the proof.
I also learned way too much about Dafny and its quirks. For instance, I originally used nats (nonnegative integers) instead of ints in the proof, but most of my variables are supposed to be positive, not just nonnegative, so that added a redundant constraint that caused performance problems. Also, Dafny is incredibly bad at reasoning about integer division due to Z3 reasons, which is why I never explicitly used the number theory properties about how lsb(i) is the largest power of 2 that divides i. For example, Dafny can’t even automatically prove this lemma and I have no idea how to prove it either:
lemma its_obvious(a: int, b: int)
requires a > 0 && b > 0
ensures a * b / b == a
{
}
Remember Kublai’s question at the beginning? Sure, Dafny can indeed verify nontrivial programs, but how practically useful is it? If it takes 350 lines to prove 10 lines of code, is this even worth it? (And it takes Dafny 7 seconds on my laptop to verify that the proof is correct!) Well first of all, Fenwick trees are quite the exception and pack a massive punch in a concise form, so something easier like ICan’tBelieveItCanSort only takes twice as many lines of proof as lines of code. Also, compared to more math-oriented theorem provers like Lean, Dafny makes it fun and ergonomic to verify imperative programs, since it automates a lot of the tedious steps for you, such as doing automatic induction. It also doesn’t have a huge learning curve, fortunately. A month ago, I knew exactly nothing about Dafny, and here I am today. So yes, proof assistants can definitely do lots of amazing things, but don’t expect to be able to verify gigantic software and eradicate all your bugs.
Challenges
Challenges left to Kublai or the reader (★ indicates difficulty):
- ★☆☆ Are the properties
0 < lsb(i) <= iand2 * lsb(i) <= lsb(i + lsb(i))enough to uniquely determine thelsbfunction? We only reasoned aboutlsbusing its various lemmas, so are there other valid Fenwick trees using differentlsbfunctions? Reader feedback: No,lsb(i) = isatisfies those two properties so we need more to uniquely pin downlsb. However, this failslsb_nextso does adding that lemma determinelsb? - ★☆☆ Mathematically prove
lsb_bad_parand that the three magic loop invariants specify the values of all the elements ofF. - ★☆☆ Prove the time complexity of the Fenwick tree operations using Dafny. Solution
- ★☆☆ Implement range queries and prove its correctness. Solution
- ★★☆ Implement prefix search and prove it. Solution
- ★★☆ Implement point updates and range queries and prove it.
- ★★★ Implement range updates and range queries and prove it.
- ★★☆ Optimize or refactor the constructor to not require
{:isolate_assertions}or use fewer RUs. - ★★★ Formally verify segment trees with lazy propagation. (Partially completed by Dipesh Kafle using Lean)
- ★★☆ Fold an origami rabbit.

Kublai: Hey! I didn’t ask for this!
Please let me know if you complete any of these challenges!
Bonus: Proving 0 == 1
I think this is a Dafny bug since it verifies and compiles this code without any errors…
// Largest power of 2 that divides i
function lsb(i: nat): nat
requires i > 0
ensures 0 < lsb(i) <= i
{
if i % 2 == 1 then 1 else 2 * lsb(i / 2)
}
opaque ghost function sum(s: seq<int>): int
{
if |s| == 0 then 0 else s[0] + sum(s[1..])
}
class fenwick {
var N: nat
ghost var A: seq<int>
var F: array<int>
constructor (A': seq<int>)
ensures F.Length == |A'| + 1
ensures F.Length > 0
ensures F.Length > 0 ==> false
ensures false
{
N := |A'|;
A := A';
F := new int[|A'| + 1](i => if 0 < i <= |A'| then A'[i - 1] else 0);
new;
for i := 1 to F.Length
modifies F
// These invariants are complete garbage and wrong
invariant forall j :: i < j <= N && j - lsb(j) / 2 >= i ==> F[j] == A[j - 1]
invariant forall j :: 0 < j <= i <= N ==> lsb(j) > 0 && F[j] == sum(A[j - lsb(j)..j])
invariant forall j :: 0 < j < i && i <= j + lsb(j) <= N ==> lsb(j) <= lsb(j + lsb(j)) && F[j + lsb(j)] == A[j + lsb(j) - 1] + sum(A[j + lsb(j) - lsb(j + lsb(j))..j])
invariant i > 0 ==> false
{
var j := i + lsb(i);
if j < F.Length {
F[j] := F[j] + F[i];
assert F[j] == A[j - 1];
assert false;
}
assert false;
}
assert F.Length > 0 ==> false;
}
}
method Main()
ensures false
{
var FT := new fenwick([0]);
assert false;
assert 0 == 1;
assert FT.N == 69;
print FT.N; // Actually prints 1
}
I initially expected Dafny to be 100% reliable and if Dafny says your proof is correct, then it’s correct. I wasn’t even intentionally trying to prove false3, but somehow it happened! But other people have also found ways to prove false in Dafny, such as this paper or if you search for “proving false” in the Dafny issue tracker, so maybe I shouldn’t put so much trust in Dafny. Welp I guess everything has bugs then. I reported this bug so I’m curious to see what happens next.
My static site generator is missing syntax highlighting support for Dafny and doesn’t support adding custom languages, so I wrote a tiny Python script that generated a Markdown file with a Dafny snippet highlighted using every supported language (Tip: Use Ctrl-click to highlight a subarray of an HTML table) and skimmed through the rendered page to find the language that makes Dafny code look the best. Actually it was more complicated than this, since there are a gazillion supported languages and the Markdown file took forever to convert to HTML and I had to split it into three parts. Anyways, turns out the answer is F#. ↩︎
I sometimes vaguely describe Dafny as “automatically filling in the missing proof steps” but a more accurate mental model is that Dafny converts the code into an intermediate language called Boogie, generates a bunch of verification conditions and then passes it to the Z3 SMT solver. ↩︎
No relation to the webcomic Proof of False. ↩︎